Integral Formulas – Integration can be considered the reverse process of differentiation or called Inverse Differentiation. Integration is the process of finding a function with its derivative. Basic integration formulas on different functions are mentioned here. Apart from the basic integration formulas, classification of integral formulas and a few sample questions are also given here, which you can practice based on the integration formulas mentioned in this article. When we speak about integration by parts, it is about integrating the product of two functions, say y = uv. More integral calculus concepts are given, so keep learning integral formulas to solve problems accurately. Also, watch the video given below to clear your concept.
List of Integral Formulas
The list of basic integral formulas are
- ∫ 1 dx = x + C
- ∫ a dx = ax+ C
- ∫ xn dx = ((xn+1)/(n+1))+C ; n≠1
- ∫ sin x dx = – cos x + C
- ∫ cos x dx = sin x + C
- ∫ sec2x dx = tan x + C
- ∫ csc2x dx = -cot x + C
- ∫ sec x (tan x) dx = sec x + C
- ∫ csc x ( cot x) dx = – csc x + C
- ∫ (1/x) dx = ln |x| + C
- ∫ ex dx = ex+ C
- ∫ ax dx = (ax/ln a) + C ; a>0, a≠1
These integral formulas are equally important as differentiation formulas. Some other important integration formulas are:
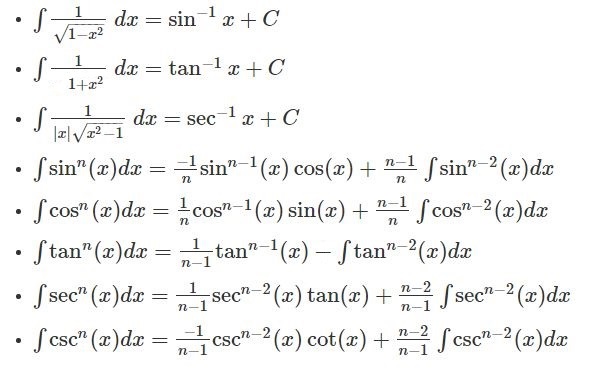
| Also, check: |
Classification of Integral Formulas
The above listed integral formulas are classified based on following functions.
- Rational functions
- Irrational functions
- Trigonometric functions
- Inverse trigonometric functions
- Hyperbolic functions
- Inverse hyperbolic functions
- Exponential functions
- Logarithmic functions
- Gaussian functions
Click here to download the PDF of important integral formulas.
Download Integral Formulas PDF
As we have already gone through integral formulas for exponential functions, logarithmic functions, trigonometric functions and some basic functions. Let’s have a look at the additional integration formulas, i.e. the integral formulas for some special functions listed below:
- \(\begin{array}{l}\int \frac{1}{(x^2 – a^2)} dx = \frac{1}{2a}.log\left | \frac{(x – a)}{(x + a)} \right | + C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{(a^2 – x^2)} dx = \frac{1}{2a}.log\left | \frac{(a + x)}{(a – x)} \right | + C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{(x^2 + a^2)} dx = \frac{1}{a}tan^{-1}(\frac{x}{a}) + C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{\sqrt{x^2 – a^2}} dx = log|x+ \sqrt{x^2 – a^2}|+ C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{\sqrt{a^2 – x^2}} dx = sin^{-1}(\frac{x}{a})+ C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{\sqrt{x^2 +a^2}} dx = log|x+ \sqrt{x^2 + a^2}|+ C\end{array} \)
Solve Using Integral Formulas
1. Calculate ∫ 5x4 dx
2. Find
3. Solve


No need of other formula than it
Great job
Very usefull for students
Very good 🙂 I am proud of you:))))
Thank u so much