A parabola is a U-shaped plane curve where any point is at an equal distance from a fixed point (known as the focus) and from a fixed straight line which is known as the directrix. Parabola is an integral part of conic section topic and all its concepts parabola are covered here.
TABLE OF CONTENTS
- Definition
- Standard Equation
- Latus Rectum
- Parametric co-ordinates
- General Equations
- Tangent to a Parabola
- Normal to a Parabola
- Focal Chord Properties
- Focal Chord, Tangent and Normal Properties
- Forms
- Questions
Download this lesson as PDF:-Parabola PDF
What is Parabola?
Section of a right circular cone by a plane parallel to a generator of the cone is a parabola. It is a locus of a point, which moves so that distance from a fixed point (focus) is equal to the distance from a fixed line (directrix)
- Fixed point is called focus
- Fixed line is called directrix

Standard Equation of Parabola
The simplest equation of a parabola is y2 = x when the directrix is parallel to the y-axis. In general, if the directrix is parallel to the y-axis in the standard equation of a parabola is given as:
| y2 = 4ax |
If the parabola is sideways i.e., the directrix is parallel to x-axis, the standard equation of a parabole becomes,
| x2 = 4ay |
Apart from these two, the equation of a parabola can also be y2 = 4ax and x2 = 4ay if the parabola is in the negative quadrants. Thus, the four equations of a parabola are given as:
-
- y2 = 4ax
- y2 = – 4ax
- x2 = 4ay
- x2 = – 4ay
Parabola Equation Derivation
In the above equation, “a” is the distance from the origin to the focus. Below is the derivation for the parabola equation. First, refer to the image given below.

From definition,
SP = PM
(x – a)2 + y2 = (x + a)2
Latus Rectum of Parabola
The latus rectum of a parabola is the chord that passes through the focus and is perpendicular to the axis of the parabola.

LSL’ Latus Ractum
=
= 4a (length of latus Rectum)
Note: – Two parabola are said to be equal if their latus rectum are equal.
Parametric co-ordinates of Parabola
For a parabola, the equation is y2 = -4ax. Now, to represent the co-ordinates of a point on the parabola, the easiest form will be = at2 and y = 2at as for any value of “t”, the coordinates (at2, 2at) will always satisfy the parabola equation i.e. y2 = 4ax. So,
Any point on the parabola
y2 = 4ax (at2, 2at)
where ‘t’ is a parameter.
Video Lesson on Parabola

Conormal Points of a Parabola

Properties of Tangents to a Parabola

Position of a Point with respect to Parabola

Focal Chord and Focal Distance
Focal chord: Any chord passes through the focus of the parabola is a fixed chord of the parabola.

Focal Distance: The focal distance of any point p(x, y) on the parabola y2 = 4ax is the distance between point ‘p’ and focus.

PM = a + x
PS = Focal distance = x + a
General Equations of Parabola
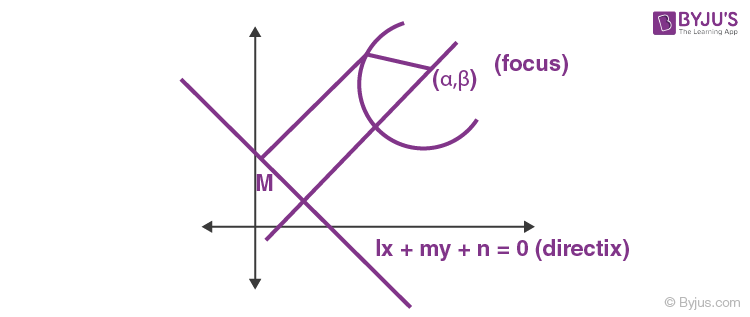
Equation of parabola by definition.
SP = PM
The general equation of 2nd degree i.e. ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 if
Position of a point with respect to parabola
For parabola
Intersection of a straight line with the parabola y2 = 4ax
Straight line y = mx + c
m slope of straight line
(mx + c)2 – 4ax = 0
m2x2 + 2x(mc – 2a) + c2 = 0
Ax2 Bx + c = 0
B2 – 4AC = discriminant D
D = 0
D > 0
mc – a > 0: Straight line intersect the curve
D < 0 (mc – a) < 0: Straight line not touching the curve
Tangent to a Parabola
Tangent at point (x1, y1)
y2 = 4ax (parabola)
equation of Tangent
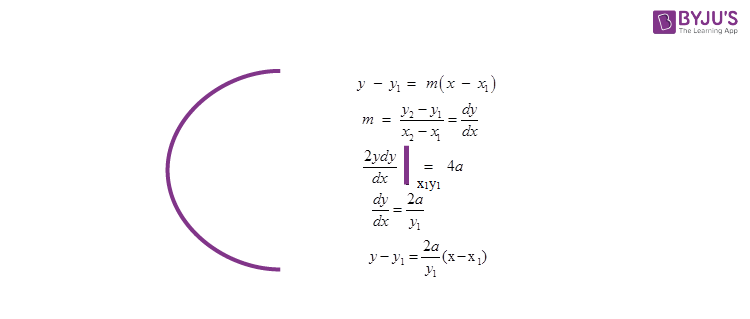
⇒ Point
Tangent in slope (m) form:
y2 = 4ax
Let equation of Tangent y = mx + c
From the previous illustration
y = mx + c touches curve at a point
so ,
equation of Tangent :- y = mx +
so, point of Tangency is
Tangent in parameter form (at2, 2at)
ty = x + at2 where ‘t’ is
parameter
Pair of Tangents from (x1, y1) external points
Let y2 = 4ax, (parabola)
P(x1, y1) external point then equation of Tangents is given by
SS1 = T2
Chord of contact:
Equation of chord of contact of Tangents from a point p(x1, y1) to the parabola y2 = 4ax is given by T = 0
i.e., yy1 – 2a(x + x1) = 0

Equation of QS T = 0
Normal to the parabola:
Normal to the point p(x1, y1) since normal is perpendicular to Tangent so slope of normal be will
slope of normal at ‘p’ (x1 y1) is
equation of normal
Normal in term of ‘m’:
Equation of normal at point (am2, – 2am)
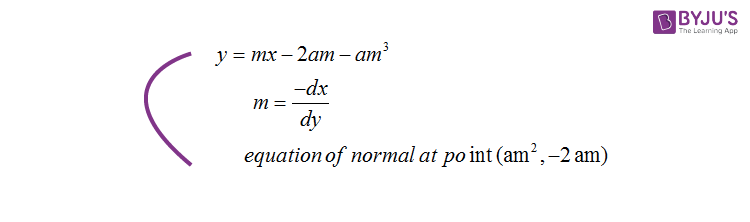
Normal at point (at2, 2at)
T parameter
y = tx + 2at + at3
Important Properties of Focal Chord
- If chord joining \(\begin{array}{l}P=(at_{1}^{2},2a{{t}_{1}})\end{array} \)and\(\begin{array}{l}Q=(at_{2}^{2},2a{{t}_{2}})\end{array} \)is focal chord of parabola\(\begin{array}{l}{{y}^{2}}=4ax\end{array} \)then\(\begin{array}{l}{{t}_{1}}{{t}_{2}}=-1\end{array} \).
- If one extremity of a focal chord is \(\begin{array}{l}(at_{1}^{2},2a{{t}_{1}})\end{array} \)then the other extremity\(\begin{array}{l}(at_{1}^{2},2a{{t}_{2}})\end{array} \)becomes\(\begin{array}{l}\left( \frac{a}{t_{1}^{2}},-\frac{2a}{{{t}_{1}}} \right)\end{array} \).
- If point \(\begin{array}{l}P(a{{t}^{2}},2at)\end{array} \)lies on parabola\(\begin{array}{l}{{y}^{2}}=4ax\end{array} \), then the length of focal chord PQ is\(\begin{array}{l}a{{(t+1/t)}^{2}}\end{array} \).
- The length of the focal chord which makes an angle θ with positive x-axis is \(\begin{array}{l}4a\cos e{{c}^{2}}\theta\end{array} \).
- Semi latus rectum is harmonic mean of SP and SQ, where P and Q are extremities of latus rectum. i.e., \(\begin{array}{l}2a=\frac{2SP\times SQ}{SP+SQ}\,or\frac{1}{SP}+\frac{1}{SQ}=\frac{1}{a}\end{array} \)
- Circle described on focal length as diameter touches tangent at vertex.
 Circle described on focal chord as diameter touches directrix.
Circle described on focal chord as diameter touches directrix.
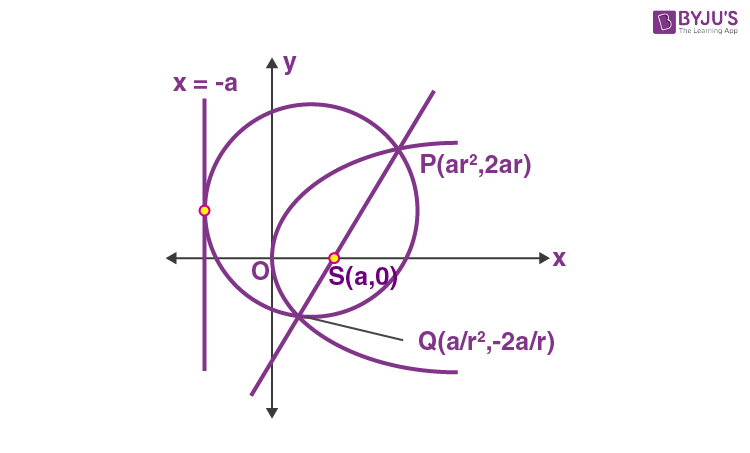
Important Properties of focal chord, Tangent and normal of Parabola
- The tangent at any point P on a parabola bisects the angle between the focal chord through P and the perpendicular from P on the directix.

- The portion of a tangent to a parabola cut off between the directrix and the curve subtends a right angle at the focus.

- Tangents at the extremities of any focal chord intersect at right angles on the directrix.

- Any Tangent to a parabola and perpendicular on it from the focus meet on the Tangent at its vertex.
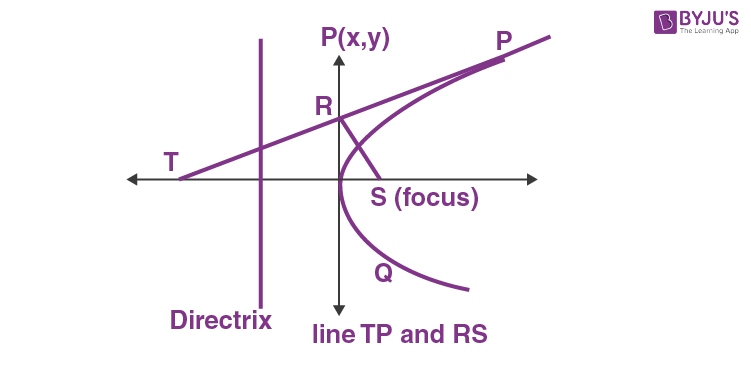
Intersect at y-axis, at u = 0
Four Common Forms of a Parabola:
| Form: | y2 = 4ax | y2 = – 4ax | x2 = 4ay | x2 = – 4ay |
|---|---|---|---|---|
| Vertex: | (0, 0) | (0,0) | (0, 0) | (0, 0) |
| Focus: | (a, 0) | (-a, 0) | (0, a) | (0, -a) |
| Equation of the directrix: | x = – a | x = a | y = – a | y = a |
| Equation of the axis: | y = 0 | y = 0 | x = 0 | x = 0 |
| Tangent at the vertex: | x = 0 | x = 0 | y = 0 | y = 0 |
Equations of Normal to a Parabola

Tangent to a Parabola

Practice Problems on Parabola
Illustration 1: Find the vertex, axis, directrix, tangent at the vertex and the length of the latus rectum of the parabola
Solution: The given equation can be re-written as
which is of the form
Hence the vertex is
The axis is
The directix is
The tangent at the vertex is
Length of the latus rectum = 4a = 2.
Illustration 2: Find the equation of the parabola whose focus is (3, -4) and directix x – y + 5 = 0.
Solution: Let P(x, y) be any point on the parabola. Then
Illustration 3: Find the equation of the parabola having focus (-6, -6) and vertex (-2, 2).
Solution: Let S(6, -6) be the focus and A(-2, 2) the vertex of the parabola. On SA take a point K (x1 , y1) such that SA = AK. Draw KM perpendicular on SK. Then KM is the directix of the parabola.
Since A bisects SK,
Hence the equation of the directrix KM is y – 10 = m(x+2) ……(1)
Also gradient of

So that equation (1) becomes
Next, let PM be a perpendicular on the directrix KM from any point P(x, y) on the parabola.
From SP = PM, the equation of the parabola is
Illustration 4: Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for
Solution: The given equation is
Here, the coefficient of x is positive. Hence, the parabola opens towards the right.
On comparing this equation with
Coordinates of the focus are given by (a, 0) i.e., (3, 0).
Since the given equation involves y2, the axis of the parabola is the y-axis.
Equation of directix is
Length of latus rectum = 4a = 4 x 3 = 12.
Illustration 5: Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for
Solution: The given equation is
Here, the coefficient of y is negative. Hence, the parabola opens downwards.
On comparing this equation with
Coordinates of the focus = (0, -a) = (0, -4).
Since the given equation involves
Equation of directrix, y = a i.e. = 4.
Length of latus rectum = 4a = 16.

Illustration 6: If the parabola y2 = 4x and x2 = 32y intersect at (16, 8) at an angle θ, then find the value of θ.
Solution: The slope of the tangent to y2 = 4x at (16, 8) is given by
The slope of the tangent to x2 = 32y at (16, 8) is given by
∴
Illustration 7: Find the equation of common tangent of y2 = 4ax and x2 – 4ay.
Solution: Equation of tangent to y2 = 4ax having slope m is
It will touch x2 – 4ay, if

Thus,
Thus, common tangent is y + x + a = 0.
Illustration 8: Find the equation of normal to the parabola y2 = 4x passing through the point (15, 12).
Solution: Equation of the normal having slope m is
If it passes through the point (15, 12) then
Hence, equations of normal are:
Illustration 9: Find the point on y2 = 8x where line x + y = 6 is a normal.
Solution: Slope m of the normal x + y = 6 is -1 and a = 2
Normal to parabola at point (am2, -2am) is
Illustration 10: Tangents are drawn to y2 = 4ax at point where the line lx + my + n = 0 meets this parabola. Find the intersection of these tangents.
Solution: Let the tangents intersects at P (h, k). Then lx + my + n = 0 will be the chord of contact. That means lx + my + n = 0 and yk – 2ax – 2ah = 0 which is chord of contact, will represent the same line.
Comparing the ratios of coefficients, we get
Illustration 11: If the chord of contact of tangents from a point P to the parabola If the chord of contact of tangents from a point P to the parabola y2 = 4ax touches the parabola x2=4by, then find the locus of P.
Solution: Chord of contact of parabola y2 = 4ax w.r.t. point P(x1 , y1)
yy1 = 2a(x + x1) ……(1)
This line touches the parabola x2 = 4by.
Solving line (1) with parabola, we have
or
According to the question, this equation must have equal roots.
Illustration 12:
Illustration 13:
(1) y^{2}=4 a x\\
(2) x^{2}=4 a y\\
(3) y^{2}=-4 a x\\
(4) x^{2}=-4 ay\\
Solution: \\
\text \ Let \ the \ point \ is \ (\mathrm{h}, \mathrm{k}). \\
\text { The equation of any normal to the parabola } \mathrm{y}^{2}=4 \mathrm{ax} \ is\\
y=m x-2 a m-a m^{3}\\
\text {Passes through ( h, k)}\\
\begin{array}{l}
k=m k-2 a m-a m^{3} \\
a m^{3}+m(2 a-h)+k=0
\end{array}\\
\mathrm{m}_{1}, \mathrm{~m}_{2}, \mathrm{~m}_{3} \text { are roots of the equation}\\
m_{1} m_{2} m_{3}=-\frac{k}{a}\\
m_{1} m_{2}=2, m_{3}=-\frac{k}{2 a}\\
\mathrm{m}_{3} \text \ is \ root \ of \ (i)\\
a\left(-\frac{k}{2 a}\right)^{3}-\frac{k}{2 a}(2 a-h)+k=0 \Rightarrow k^{2}=4 a h\\
\text {Thus locus is }y^{2}=4 a x\\
Answer: [1]\end{array} \)
Illustration 14:
Real-life applications of a Parabola
1] A liquid is rotated and the forces of gravity in the liquid are responsible for the formation of a parabola. For example when any juice is stirred round along its axis. The level of the juice increases around the edges while it slightly falls in the centre of the glass.
2] The concept of the parabola is used in satellite dishes which helps to reflect the signals and then go to the receiver. Due to parabola’s reflective properties, the signals that go to the satellite will mirror off and back to the receiver soon after reflecting off the focus.
3] The Golden Gate Bridge cables that act as a suspension are parabolas.
4] Water in The Bellagio’s fountains in Las Vegas are exhibited in the shape of parabolas.
5] The reflective properties of parabolas are used in some heaters. The source of heat is at the focus and the heat
is focused in the form of parallel rays.
6] Parabolas are applied in the field of architecture and engineering projects. Parabolic shapes include:
a] The Parabola, a structure in London built in 1962 that consists of a roof made of copper with parabolic and hyperbolic lines.
b] There exists parabolas on each side of its side spans on The Golden Gate Bridge in San Francisco, California.
7] The use of parabolas are extensive when the light needs to be focused. A parabola-shaped reflector helps in focusing light into a beam that can be seen from long distances. It helps in reducing more usage of light and thus improves the surface of the parabola.
8] Solar power industry is aided by the parabolic reflectors to concentrate light.
9] The most frequent example of a parabola is that of the stretched arc of a rocket launch.
10] The parabolic trajectories are in use from decades.
Parabola Solved Questions


 Circle described on focal chord as diameter touches directrix.
Circle described on focal chord as diameter touches directrix.


good and best to get suceed in a chapter