Completing The Square Method

A polynomial equation with a degree equal to two is known as a quadratic equation. ‘Quad’ means four, but ‘Quadratic’ means ‘to make square’. A quadratic equation in its standard form is represented as:

ax² + bx + c = 0, where a, b and c are real numbers such that a ≠ 0 and x is a variable.

Since the degree of the above-written equation is two, it will have two roots or solutions. The roots of polynomials are the values of x, which satisfy the equation. There are several methods to find the roots of a quadratic equation. One of them is by completing the square. The ways of solving these quadratics have been introduced to the students in Class 10 and 11. In this article, you can learn how to solve a given quadratic equation using the method of completing the square.

Completing The Square Method

Completing the square method is one of the methods to find the roots of the given quadratic equation. In this method, we have to convert the given equation into a perfect square. We can also evaluate the roots of the quadratic equation by using the quadratic formula.

Completing the Square for Quadratic Equation

For completing the square to solve quadratic equations, first we need to write the standard form as:

ax² + bx + c = 0

For simplification, let us take a = 1 so that the equation becomes,

x² + bx + c = 0

If we wanted to represent a quadratic equation using geometry, one way would be to describe the terms of the expression in the L.H.S. of the equation using geometric figures such as squares, rectangles etc. If we take a square with the side equal to x units, its area would be equivalent to x² square units. This area will hence represent the first term of the expression. Similarly, a rectangle with its two sides as x units and b units will have an area equal to bx square units. And let us take a square with an area equal to c square units to represent the last term of the expression. In the figure below, we have the geometrical equivalent of the expression x², bx and c.

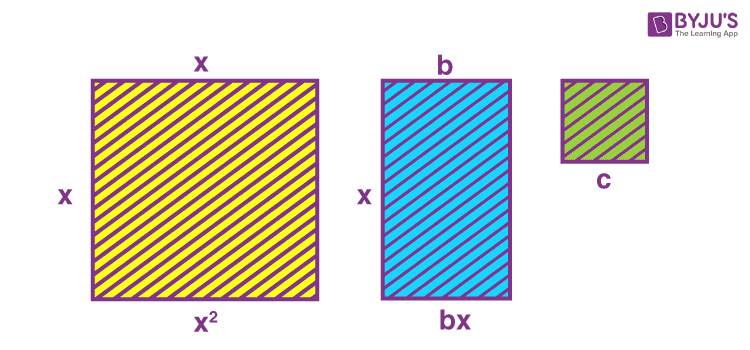
Geometrical equivalent of x², bx and c

Let us complete some squares as mentioned in the previous figure. If we break the rectangle representing bx into two equal parts, cutting vertically, we will have two figures with an area of each equal to b/2 x square units. The figures are arranged accordingly in the second figure below.

Rearranging the figures

But our square is not complete yet. One square of side b/2 units is needed to complete the square shape. We can take this final part of the main square from the square with the area c square units. After cutting it out and putting it in place, it results in the below figure.

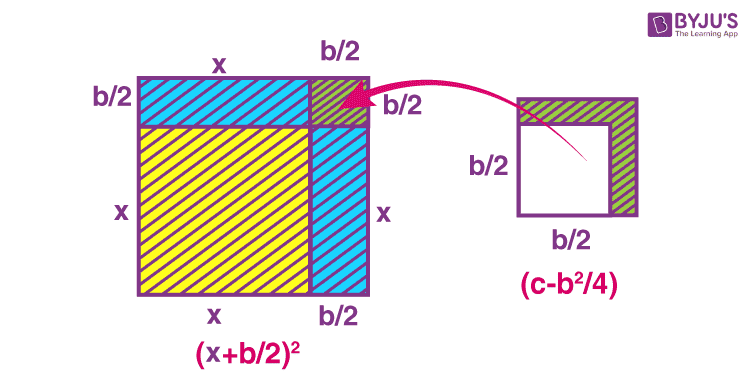
Let us derive the formula for completing the square with the help of the above procedure.

Completing The Square Formula

The square is finally completed in the above figure. The area of the square is equal to

(x + b/2)² square units

The remaining area is equal to

(c – b²/4) square units

All this time, we were rearranging the same figures that we had initially. Thus, the actual representation can be:

x² + bx + c = (x + b/2)² + (c – b²/4)

This method is known as completing the square method. We have achieved it geometrically. 

We know that, 

x² + bx + c = 0

This can be written as:

(x + b/2)² + (c – b²/4) = 0

⇒ (x + b/2)² = -(c – b²/4)

This formula can be used to solve the quadratic equations by completing the square technique.

All the terms in the R.H.S. of the above equation are known. That’s why it is easy to determine the roots. 

Steps for Completing the square method

Suppose ax² + bx + c = 0 is the given quadratic equation. Then follow the given steps to solve it by completing the square method.

Step 1: Write the equation in the form, such that c is on the right side.

Step 2: If a is not equal to 1, divide the complete equation by a such that the coefficient of x² will be 1.

Step 3: Now add the square of half of the coefficient of term-x, (b/2a)², on both sides.

Step 4: Factorize the left side of the equation as the square of the binomial term.

Step 5: Take the square root on both the sides

Step 6: Solve for variable x and find the roots.

The above steps can be implemented as shown below.

Consider the quadratic equation ax² + bx + c = 0 (a ≠ 0). 

Dividing throughout by a, we get

x² + (b/a)x + (c/a) = 0

This can also be written by adding and subtracting (b/2a)² as,

[x + (b/2a)]² – (b/2a)² + (c/a) = 0

[x + (b/2a)]² – [(b² – 4ac)/4a²] = 0

[x + (b/2a)]² = [(b² – 4ac)/4a²]

If b² – 4ac ≥ 0, then by taking the square root, we get

x + (b/2a) = ± √(b² – 4ac)/ 2a

Further simplification of this will give you the quadratic formula.

Otherwise, we can directly apply the completing the square method formula while solving the equations.

Let us look at some examples for better understanding of this technique.

Completing the Square Examples

Example 1: Find the roots of the quadratic equation x² + 4x – 5 = 0 by the method of completing the square.

Solution:

Given quadratic equation is:

x² + 4x – 5 = 0

Comparing the equation with the standard form,

b = 4, c = -5

(x + b/2)² = -(c – b²/4)

So, [x + (4/2)]² = -[-5 – (4²/4)]

(x + 2)² = 5 + 4

⇒ (x + 2)² = 9

⇒ (x + 2) = ±√9

⇒ (x + 2) = ± 3

⇒ x + 2 = 3, x + 2 = -3

⇒ x = 1 , -5

Therefore, the roots of the given equation are 1 and -5.

Example 2: Find the roots of the quadratic equation 3x² – 5x + 2 = 0 by completing the square.

Solution:

Given quadratic equation is:

3x² – 5x + 2 = 0

The given equation is not in the form to which we apply the method of completing squares, i.e. the coefficient of x² is not 1. To make it 1, we need to divide the whole equation with 3.

x² – 5/3 x + 2/3 = 0

Comparing with the standard form,

b = -5/3; c = ⅔

c – b²/4 = ⅔ – [(5/3)²/4] = (2/3) – (25/36) = (24 – 25)/36 =  -1/36

Substituting these values in the equation (x + b/2)² = -(c – b²/4) we get,

⇒ (x – 5/6)² = 1/36

⇒ (x – 5/6)= ± √(1/36)

⇒ x – 5/6 = ±1/6

⇒ x = 1, -2/3

Therefore, the roots of the given equation are 1 and -⅔.

The below video will help you visualize the concepts of solving quadratic equations.

Completing the Square Problems

Let’s practice the questions on completing the square method of solving quadratic equations.

1. Find the roots of 4x² + 3x + 5 = 0 by the method of completing the square.
2. Find the roots of the equation 5x² – 6x – 2 = 0 by the method of completing the square.
3. Find two consecutive odd positive integers, the sum of whose squares is 290.

To solve more problems on the topic, download BYJU’S – The Learning App from Google Play Store.