Decimal Expansion Of Rational Numbers

Before going into a representation of the decimal expansion of rational numbers, let us understand what rational numbers are. Any number that can be represented in the form of p/q, such that p and q are integers and q ≠ 0 are known as rational numbers. So when these numbers have been simplified further, they result in decimals. Let us learn how to expand such decimals here.

Examples:

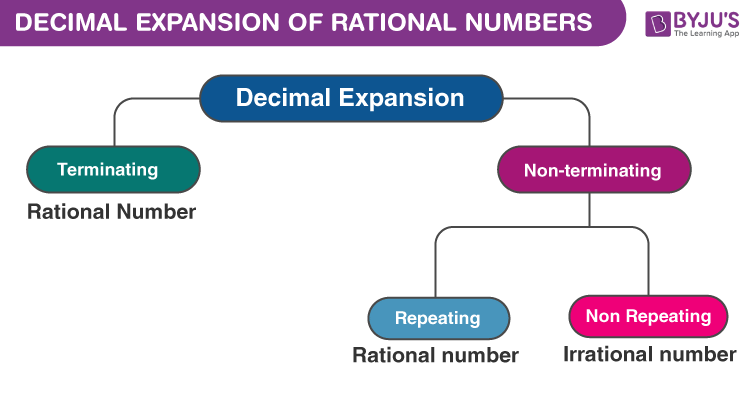
How to Expand Rational Numbers in Decimals?

The real numbers which are recurring or terminating in nature are generally rational numbers.

For example, consider the number 33.33333……. It is a rational number as it can be represented in the form of 100/3. It can be seen that the decimal part .333…… is the non-terminating repeating part, i .e. it is a recurring decimal number.

Also the terminating decimals such as 0.375, 0.6 etc. which satisfy the condition of being rational (

Consider any decimal number. For e.g. 0.567. It can be written as 567/1000 or

Thus, it can be seen that any decimal number can be represented as a fraction which has denominator in powers of 10. We know that prime factors of 10 are 2 and 5, it can be concluded that any decimal rational number can be easily represented in the form of

This statement gives rise to a very important theorem.

Theorems

Theorem 1: If m be any rational number whose decimal expansion is terminating in nature, then m can be expressed in form of

The converse of this theorem is also true and it can be stated as follows:

Theorem 2: If m is a rational number, which can be represented as the ratio of two integers i.e.

Consider the following examples:

1. \(\begin{array}{l}\frac{7}{8}\end{array} \)
   =
   \(\begin{array}{l}\frac{7}{2^3}\end{array} \)
   =
   \(\begin{array}{l}\frac{7~×~5^3}{2^3~×~5^3}\end{array} \)
   =
   \(\begin{array}{l}\frac{875}{10^3}\end{array} \)
2. \(\begin{array}{l}\frac{3}{80}\end{array} \)
   =
   \(\begin{array}{l}\frac{3}{2^4~×~5}\end{array} \)
   =
   \(\begin{array}{l}\frac{3~×~5^3}{2^4~×~5^4}\end{array} \)
   =
   \(\begin{array}{l}\frac{375}{10^4}\end{array} \)

Moving on, to decimal expansion of rational numbers which are recurring, the following theorem can be stated:

Theorem 3: If m is a rational number, which can be represented as the ratio of two integers i.e.

Consider the following examples:

1. \(\begin{array}{l}\frac{1}{6}\end{array} \)
   =
   \(\begin{array}{l}0.1666….\end{array} \)
   =
   \(\begin{array}{l}0.1\overline{6}\end{array} \)
2. \(\begin{array}{l}\frac{7}{12}\end{array} \)
   =
   \(\begin{array}{l}0.58333…\end{array} \)
   =
   \(\begin{array}{l}0.58\overline{3} \end{array} \)
3. \(\begin{array}{l}\frac{9}{11}\end{array} \)
   =
   \(\begin{array}{l}0.8181…\end{array} \)
   =
   \(\begin{array}{l}0.\overline{81}\end{array} \)

Rational Number to decimal Examples

Case 1: Remainder equal to zero

Example: Find the decimal expansion of 3/6.

Here, the quotient is 0.5 and the remainder is 0. Rational number 3/6 results in a terminating decimal.

Case 2: Remainder not equal to zero 

Example: Express 5/13 in decimal form.

Here, the quotient is 0.384615384 and the remainder is not zero. Notice that the number…384 after the decimal is repeating. Hence, 5/13 gives us a non-terminating recurring decimal expansion. And this can be written as 5/13=

A rational number gives either terminating or non-terminating recurring decimal expansion. Thus, we can say that a number whose decimal expansion is terminating or non-terminating recurring is rational. 

Find the joy in learning with us. To know more about rational numbers please visit our website www.byjus.com and download BYJU’S-The Learning App from Google play store to learn anytime anywhere.