The value of sin 30 degrees is 0.5. Sin 30 is also written as sin π/6, in radians. The trigonometric function also called as an angle function relates the angles of a triangle to the length of its sides. Trigonometric functions are important, in the study of periodic phenomena like sound and light waves, average temperature variations and the position and velocity of harmonic oscillators and many other applications. The most familiar three trigonometric ratios are sine function, cosine function and tangent function.
| Sine 30°=1/2 |
For angles less than a right angle, trigonometric functions are commonly defined as the ratio of two sides of a right triangle. The angles are calculated with respect to sin, cos and tan functions. Usually, the degrees are considered as 0°, 30°, 45°, 60°, 90°, 180°, 270° and 360°. Here, we will discuss the value for sin 30 degrees and how to derive the sin 30 value using other degrees or radians.
Sine 30 Degrees Value
The exact value of sin 30 degrees is ½. To define the sine function of an angle, start with a right-angled triangle ABC with the angle of interest and the sides of a triangle. The three sides of the triangle are given as follows:
- The opposite side is the side opposite to the angle of interest.
- The hypotenuse side is the side opposite the right angle and it is always the longest side of a right triangle
- The adjacent side is the side adjacent to the angle of interest other than the right angle
The sine function of an angle is equal to the length of the opposite side divided by the length of the hypotenuse side and the formula is given by:
Sine Law: The sine law states that the sides of a triangle are proportional to the sine of the opposite angles.
The sine rule is used in the following cases :
Case 1: Given two angles and one side (AAS and ASA)
Case 2: Given two sides and non included angle (SSA)
The other important sine values with respect to angle in a right-angled triangle are:
Sin 0 = 0
Sin 45 = 1/√2
Sin 60 = √3/2
Sin 90 = 1
Fact: The values sin 30 and cos 60 are equal.
Sin 30 = Cos 60 = ½
And
Cosec 30 = 1/Sin 30
Cosec 30 = 1/(½)
Cosec 30 = 2
Derivation to Find the Sin 30 value (Geometrically)
Let us now calculate the sin 30 value. Consider an equilateral triangle ABC. Since each angle in an equilateral triangle is 60°, therefore
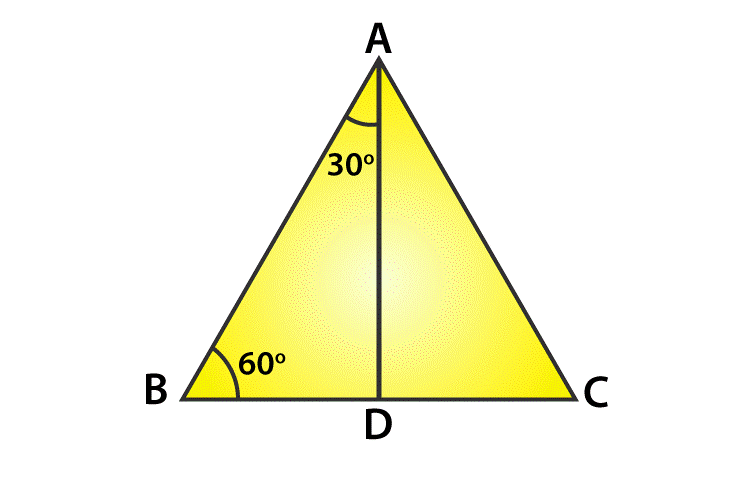
Draw the perpendicular line AD from A to the side BC (From figure)
Now
Therefore BD=DC and also
Now observe that the triangle ABD is a right triangle, right-angled at D with
As you know, for finding the trigonometric ratios, we need to know the lengths of the sides of the triangle. So, let us suppose that AB=2a
To find the sin 30-degree value, let’s use sin 30-degree formula and it is written as:
Sin 30° = opposite side/hypotenuse side
We know that, Sin 30° = BD/AB = a/2a = 1 / 2
Therefore, Sin 30 degree equals to the fractional value of 1/ 2.
Sin 30° = 1 / 2
Therefore, sin 30 value is 1/2
In the same way, we can derive other values of sin degrees like 0°, 30°, 45°, 60°, 90°,180°, 270° and 360°. Below is the trigonometry table, which defines all the values of sine along with other trigonometric ratios.
| Related Links | |
| Sin 0 Degree | Trigonometry Formulas |
| Inverse Cosine | Law of Sines Formula |
Why Sin 30 is equal to Sin 150
The value of sin 30 degrees and sin 150 degrees are equal.
Sin 30 = sin 150 = ½
Both are equal because the reference angle for 150 is equal to 30 for the triangle formed in the unit circle. The reference angle is formed when the perpendicular is dropped from the unit circle to the x-axis, which forms a right triangle.
Since, the angle 150 degrees lies on the IInd quadrant, therefore the value of sin 150 is positive.The internal angle of triangle is 180 – 150=30, which is the reference angle.
The value of sine in other two quadrants, i.e. 3rd and 4th are negative.
In the same way,
Sin 0 = sin 180
Trigonometry Table
| Trigonometry Ratio Table | ||||||||
| Angles (In Degrees) | 0 | 30 | 45 | 60 | 90 | 180 | 270 | 360 |
| Angles (In Radians) | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | −1 | 0 |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | −1 | 0 | 1 |
| tan | 0 | 1/√3 | 1 | √3 | Not Defined | 0 | Not Defined | 0 |
| cot | Not Defined | √3 | 1 | 1/√3 | 0 | Not Defined | 0 | Not Defined |
| cosec | Not Defined | 2 | √2 | 2/√3 | 1 | Not Defined | −1 | Not Defined |
| sec | 1 | 2/√3 | √2 | 2 | Not Defined | −1 | Not Defined | 1 |
Solved Examples
Question 1: In triangle ABC, right-angled at B, AB = 5 cm and angle ACB = 30°. Determine the length of the side AC.

Solution:
To find the length of the side AC, we consider the sine function, and the formula is given by
Sin 30°= Opposite Side / Hypotenuse side
Sin 30°= AB / AC
Substitute the sin 30 value and AB value,
Therefore, the length of the hypotenuse side, AC = 10 cm.
Question 2: If a right-angled triangle has a side opposite to an angle A, of 6cm and hypotenuse of 12cm. Then find the value of angle.
Solution: Given, Side opposite to angle A = 6cm
Hypotenuse = 12cm
By sin formula we know that;
Sin A = Opposite side to angle A/Hypotenuse
Sin A = 6/12 = ½
We know, Sin 30 = ½
So if we compare,
Sin A = Sin 30
A = 30
Hence, the required angle is 30 degrees.
Question 3: If a right-angled triangle is having adjacent side equal to 10 cm and the measure of angle is 45 degrees. Then find the value hypotenuse of the triangle.
Solution: Given adjacent side = 10cm
We know,
Tan 45 = Opposite side/Adjacent side
Tan 45 = opposite side/10
Since, Tan 45 = 1
Therefore,
1 = Opposite side/10
Opposite side = 10 cm
Now, by sin formula, we know,
Sin A = Opposite side/Hypotenuse
So,
Sin 45 = 10/Hypotenuse
Hypotenuse = 10/sin 45
Hypotenuse = 10/(1/√2)
Hypotenuse = 10√2
Keep visiting BYJU’S for more information on trigonometric ratios and its related articles, and also watch the videos to clarify the doubts.
Frequently Asked Questions – FAQs
What is the exact value of sine 30 degrees?
What is the value of sine 30 in the form of fraction?
What is sine 30 degrees in radian?
What is the formula for sine function?
Sine A = Opposite Side/Hypotenuse
What is the value of cos 30 and tan 30?
How to find the value of tan 30 with respect to sin and cos?
Tan 30 = sin 30/cos 30
We know that, sin 30 = ½ and cos 30 = √3/2
Therefore, tan 30 = (½)/√3/2
Tan 30 = 1/√3



Very well explained.
This app is very useful for students