What are Events in Probability?
A probability event can be defined as a set of outcomes of an experiment. In other words, an event in probability is the subset of the respective sample space. So, what is sample space?
The entire possible set of outcomes of a random experiment is the sample space or the individual space of that experiment. The likelihood of occurrence of an event is known as probability. The probability of occurrence of any event lies between 0 and 1.
Events In Probability
The sample space for the tossing of three coins simultaneously is given by:
S = {(T , T , T) , (T , T , H) , (T , H , T) , (T , H , H ) , (H , T , T ) , (H , T , H) , (H , H, T) ,(H , H , H)}
Suppose, if we want to find only the outcomes which have at least two heads; then the set of all such possibilities can be given as:
E = { (H , T , H) , (H , H ,T) , (H , H ,H) , (T , H , H)}
Thus, an event is a subset of the sample space, i.e., E is a subset of S.
There could be a lot of events associated with a given sample space. For any event to occur, the outcome of the experiment must be an element of the set of event E.
What is the Probability of Occurrence of an Event?
The number of favourable outcomes to the total number of outcomes is defined as the probability of occurrence of any event. So, the probability that an event will occur is given as:
P(E) = Number of Favourable Outcomes/ Total Number of Outcomes
Types of Events in Probability:
Some of the important probability events are:
- Impossible and Sure Events
- Simple Events
- Compound Events
- Independent and Dependent Events
- Mutually Exclusive Events
- Exhaustive Events
- Complementary Events
- Events Associated with “OR”
- Events Associated with “AND”
- Event E1 but not E2
Impossible and Sure Events
If the probability of occurrence of an event is 0, such an event is called an impossible event and if the probability of occurrence of an event is 1, it is called a sure event. In other words, the empty set ϕ is an impossible event and the sample space S is a sure event.
Simple Events
Any event consisting of a single point of the sample space is known as a simple event in probability. For example, if S = {56 , 78 , 96 , 54 , 89} and E = {78} then E is a simple event.
Compound Events
Contrary to the simple event, if any event consists of more than one single point of the sample space then such an event is called a compound event. Considering the same example again, if S = {56 ,78 ,96 ,54 ,89}, E1 = {56 ,54 }, E2 = {78 ,56 ,89 } then, E1 and E2 represent two compound events.
Independent Events and Dependent Events
If the occurrence of any event is completely unaffected by the occurrence of any other event, such events are known as an independent event in probability and the events which are affected by other events are known as dependent events.
Mutually Exclusive Events
If the occurrence of one event excludes the occurrence of another event, such events are mutually exclusive events i.e. two events don’t have any common point. For example, if S = {1 , 2 , 3 , 4 , 5 , 6} and E1, E2 are two events such that E1 consists of numbers less than 3 and E2 consists of numbers greater than 4.
So, E1 = {1,2} and E2 = {5,6} .
Then, E1 and E2 are mutually exclusive.
Exhaustive Events
A set of events is called exhaustive if all the events together consume the entire sample space.
Complementary Events
For any event E1 there exists another event E1‘ which represents the remaining elements of the sample space S.
E1 = S − E1‘
If a dice is rolled then the sample space S is given as S = {1 , 2 , 3 , 4 , 5 , 6 }. If event E1 represents all the outcomes which is greater than 4, then E1 = {5, 6} and E1‘ = {1, 2, 3, 4}.
Thus E1‘ is the complement of the event E1.
Similarly, the complement of E1, E2, E3……….En will be represented as E1‘, E2‘, E3‘……….En‘
Events Associated with “OR”
If two events E1 and E2 are associated with OR then it means that either E1 or E2 or both. The union symbol (∪) is used to represent OR in probability.
Thus, the event E1U E2 denotes E1 OR E2.
If we have mutually exhaustive events E1, E2, E3 ………En associated with sample space S then,
E1 U E2 U E3U ………En = S
Events Associated with “AND”
If two events E1 and E2 are associated with AND then it means the intersection of elements which is common to both the events. The intersection symbol (∩) is used to represent AND in probability.
Thus, the event E1 ∩ E2 denotes E1 and E2.
Event E1 but not E2
It represents the difference between both the events. Event E1 but not E2 represents all the outcomes which are present in E1 but not in E2. Thus, the event E1 but not E2 is represented as
E1, E2 = E1 – E2
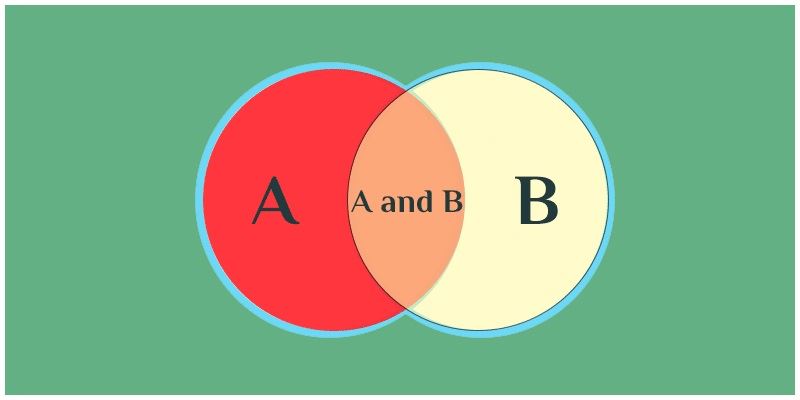
Types of Events In Probability
Example Question on Probability of Events
Question: In the game of snakes and ladders, a fair die is thrown. If event E1 represents all the events of getting a natural number less than 4, event E2 consists of all the events of getting an even number and E3 denotes all the events of getting an odd number. List the sets representing the following:
i)E1 or E2 or E3
ii)E1 and E2 and E3
iii)E1 but not E3
Solution:
The sample space is given as S = {1 , 2 , 3 , 4 , 5 , 6}
E1 = {1,2,3}
E2 = {2,4,6}
E3 = {1,3,5}
i)E1 or E2 or E3= E1 E2 E3= {1, 2, 3, 4, 5, 6}
ii)E1 and E2 and E3 = E1 E2 E3 = ∅
iii)E1 but not E3 = {2}
Probability Related Video:

More Topics Related to Probability Events
| Probability and Statistics | Probability Formulas |
| Multiplication Rule Probability | Bayes Theorem |
| Bernoulli Trials Binomial Distribution | Independent Events And Probability |
Frequently Asked Questions
What are Events in Probability?
In probability, events are the outcomes of an experiment. The probability of an event is the measure of the chance that the event will occur as a result of an experiment.
What is the Difference Between Sample Space and Event?
A sample space is a collection or a set of possible outcomes of a random experiment while an event is the subset of sample space. For example, if a die is rolled, the sample space will be {1, 2, 3, 4, 5, 6} and the event of getting an even number will be {2, 4, 6}.
What is the Probability of an Impossible Event and a Sure Event?
The probability of a sure event is always 1 while the probability of an impossible event is always 0.
What is an Example of an Impossible Event?
An example of an impossible event will be getting a number greater than 6 when a die is rolled.



The simple probability of an occurance of an event is called
A. Bayesian probability
B. Marginal probability
C. Conditional probability
D. Joint probability
I want the citation of this article!
i salute 2 u mathematician