A varying velocity results in acceleration. If an object is spinning and its speed is changing, then we say it is accelerating angularly. In this article, we will be exploring angular acceleration in detail.
|
Table of Contents |
What is Angular Acceleration?
Angular Acceleration is defined as the time rate of change of angular velocity. It is usually expressed in radians per second per second. Thus,
The angular acceleration is also known as rotational acceleration. It is a quantitative expression of the change in angular velocity per unit time.
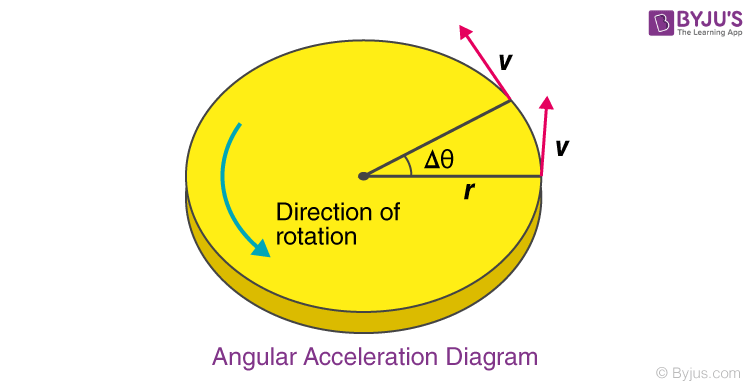
Angular Acceleration is a pseudoscalar. The sign of angular acceleration is considered positive if the angular speed increases counterclockwise, and is taken to be negative if the angular speed increases clockwise. The motion of rotating objects such as the wheel, fan and earth are studied with the help of angular acceleration.
|
Related Links: |
Angular Acceleration Unit
The vector direction of the acceleration is perpendicular to the plane where the rotation takes place. Increase in angular velocity clockwise, then the angular acceleration velocity points away from the observer. If the increase in angular velocity is counterclockwise, then the vector of angular acceleration points toward the viewer.
In SI units, angular acceleration is measured in radians per second squared (rad/s2) and is usually denoted by the alpha (α).
Angular Acceleration Formula
Angular velocity is the rate of change of angular position of a rotating body and it is represented as follows:
\(\begin{array}{l}\omega =\frac{\theta }{t}\end{array} \) |
Where,
- ω = Angular Velocity
- θ = Angle Rotated
- t = Time Taken
When the angular velocity is constant, the angular acceleration is 0. If the velocity is not constant, then the constant α is defined as:
\(\begin{array}{l}\alpha =\frac{\omega }{t}=\frac{\theta }{t^{2}}\end{array} \) |
If the angular acceleration is not constant and differs from time to time, then:
\(\begin{array}{l}\alpha_{avg}=(\frac{\omega_{2} -\omega _{1}}{t_{2}-t_{1}})\end{array} \) |
And,
\(\begin{array}{l}\alpha_{i}=\frac{d\omega }{dt}=\frac{d^{2}\theta }{dt^{2}}\end{array} \) |
Read More: Angular Acceleration Formula
Angular Acceleration Examples
1) If a rotating disc changes its angular speed at the rate of 60 rad/s for 10 seconds. Calculate its angular acceleration during this time.
Solution:
The change in angular velocity is 60 rad/s.
The time taken for this change to occur is 10 s.
Substituting the above values in the angular acceleration formula, we get:
Solving, we get
2) If the rear wheel of a bicycle has an angular acceleration of 20 rad/s<sup>2</sup>. Then what can be said about its angular velocity?
Solution:
The given angular acceleration is 20 rad/s<sup>2</sup>.
Time taken is 1 second.
Rearranging the angular acceleration formula, we get:
Substituting values in the above equation, we get:
Watch the video and learn how did the parent definition of omega ’⍵’ or angular velocity evolved.





Comments