Average Speed And Average Velocity

Before learning about average speed and average velocity, we must know the difference between distance and displacement.

Looking for other study material?

Distance is a scalar quantity which generally implies how much ground has been covered by the object. On the other hand, displacement is a vector quantity, and it is the shortest possible distance between the start and end point.

Example: If a particle is moving in a circle, after one revolution, the distance will be the perimeter of the circle while the displacement would be zero.

Now, let us see what speed and velocity actually are.

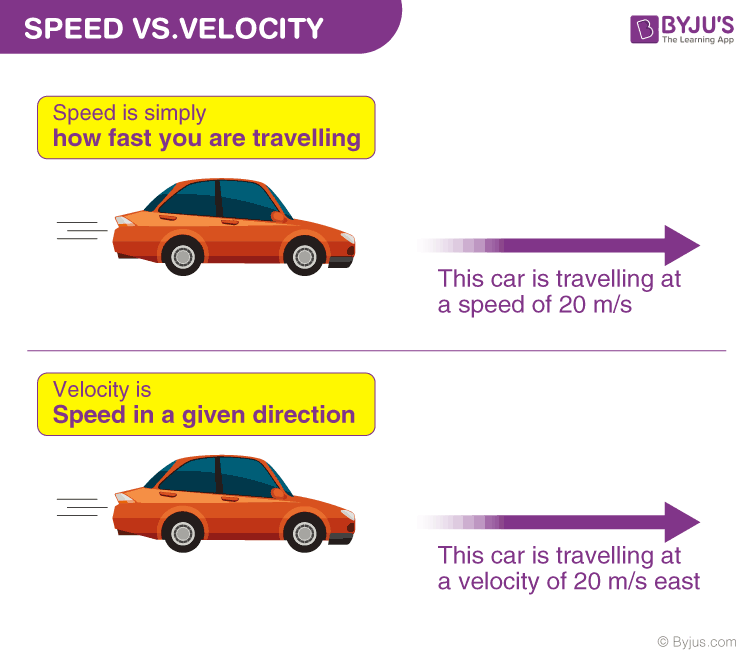
Speed: Speed is a scalar quantity which means it has no direction. It denotes how fast an object is moving. If the speed of the particle is high it means the particle is moving fast and if it is low,  it means the particle is moving slow.

Velocity: Velocity is a vector quantity which means it has both magnitude and direction. It denotes the rate at which the object is moving or changing position. The direction of the velocity vector is easy to find. Its direction is same as the direction of the moving object. Even if the object is slowing down, and the magnitude of velocity is decreasing, its direction would still be same as the direction in which the object is moving

Average Speed

The average speed of a body in a certain time interval is the distance covered by the body in that time interval divided by time. So if a particle covers a certain distance s in a time

In general, average speed formula is:

Now let us look at some of the examples to understand this concept easily

1.) In travelling from Pune to Nagpur , Rahul drove his bike for 2 hours at 60 kmph and 3 hours at 70 kmph.

Sol 1) We know that, Distance = Speed × Time

So, in 2 hours, distance covered = 2 × 60 = 120 km

in the next 3 hours, distance covered = 3 × 70 = 210 km

Total distance covered = 120 + 210 = 330 km

Total time = 2 + 3 = 5 hrs

Avg. Speed = 

Avg. Speed = 330/5 = 66 kmph

Average Velocity

The average velocity of a body in a certain time interval is given as the displacement of the body in that time interval divided by time. So if a particle covers a certain displacement

In general, the  formula is:

Understand the concept average velocity through the examples given below.

1) What is the average velocity of a person who moves 7 m in 4 seconds and 18 m in 6 seconds along x-axis?

Sol) Initial distance traveled by the person, x_i = 7 m,

Final distance traveled, x_f  = 18 m,

Initial time interval t_i = 4 sec,

Final time interval t_f = 6 sec,

Average velocity Vav = 

To learn more about Speed and Velocity, download BYJU’S- The Learning App.