What is Einstein Field Equation?
The Einstein Field Equation (EFE) is also known as Einstein’s equation. There are ten nonlinear partial differential equations of Einstein field extracted from Albert Einstein’s General Theory of Relativity. The EFE describes the basic interaction of gravitation. The equations were first published in 1915 by Albert Einstein as a tensor equation.
Following is the Einstein Field Equation:
\(\begin{array}{l}G_{\mu \upsilon } + g_{\mu \upsilon }\Lambda = \frac{8 \pi G}{c^{4}}T_{\mu \upsilon }\end{array} \) |
Where,
- Gμ? is the Einstein tensor which is given as Rμ?-½ Rgμ?
- Rμ? is the Ricci curvature tensor
- R is the scalar curvature
- gμ? is the metric tensor
- ? is a cosmological constant
- G is Newton’s gravitational constant
- c is the speed of light
- Tμ? is the stress-energy tensor
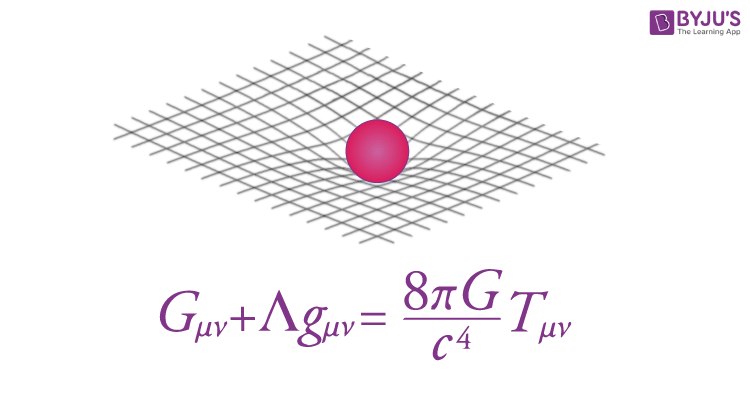
Einstein Field Equations Derivation
Following is the derivation of Einstein Field Equations. Einstein wanted to explain that measure of curvature = source of gravity.
The source of gravity is the stress-energy tensor. The stress-energy tensor is given as:
In the above matrix we see that the P is tending to zero because, for Newton’s gravity, the mass density is the source of gravity.
The equation of motion is given as:
But we know that
Therefore,
Where
What is Einstein Tensor?
Einstein tensor is also known as trace-reversed Ricci tensor. In Einstein Field Equation, it is used for describing spacetime curvature such that it is in alignment with the conservation of energy and momentum. It is defined as:
| G = R-½ gR |
Where,
- R is the Ricci tensor
- g is the metric tensor
- R is the scalar curvature
What is stress-energy tensor?
Stress-energy tensor is defined as the tensor Tαβ is a symmetrical tensor which is used for describing the energy and momentum density of the gravitational field. It is given as:
| Tαβ = Tβα |
Stay tuned with BYJU’S for more such interesting articles. Also, register to “BYJU’S – The Learning App” for loads of interactive, engaging Physics-related videos and an unlimited academic assist.




This was very helpful, thank you so much.