We often hear in the news that two vehicles collided causing injuries to people. These collisions prove to be dangerous depending on the force they collide with each other. Let us try to find out how we can define collision? So to get started collision is a situation in which interacting bodies experience large force for a short interval of time. The line along which the internal forces act during collision is known as the line of collision. Franck Hertz experiment explains about the elastic and inelastic collision.
To know about the centre of mass, click on the video below.

Types of Collision
Depending upon the velocity of the body with respect to the line of the collision, the collisions are classified into two types:
Head-on Collision:
This type of collision happens when velocities of both the particles are along the line of collision. This can be regarded as a collision in one dimension. Head-on collision is as shown in the figure.

Head-on Collision
Oblique Collision:
Oblique collision takes place when one of the two bodies have a velocity at an angle with the line of collision. In case of an oblique collision, the component of velocity perpendicular to the line of the collision remains unchanged. This can be regarded as a collision in two dimensions.
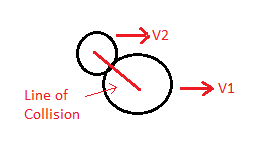
Oblique Collision
Apart from the above two classification collisions can also be classified on the basis of whether kinetic energy remains constant or not. If the kinetic energy of the system remains constant, then it is known as an elastic collision. While there are situations when some kinetic energy gets converted into heat, deformation of shape etc. These types of collision are known as an inelastic collision.
We often define another quantity known coefficient of restitution (e). It is defined as the ratio of the velocity of separation by the velocity of approach along the line of collision. So here,
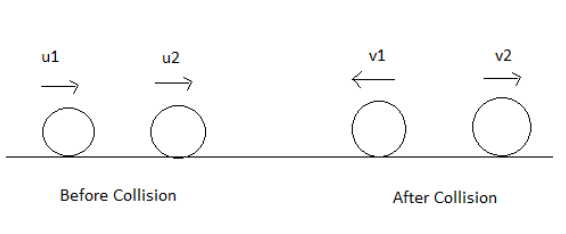
Depending on the values of e we can infer the type of collision.
For e = 1, Elastic collision
0 < e < 1, inelastic collision
e = 0, perfectly inelastic collision
Stay tuned to BYJU’S to learn more about the basics of collision.





Comments