Law of equipartition of energy: Statement
According to the law of equipartition of energy, for any dynamic system in thermal equilibrium, the total energy for the system is equally divided among the degree of freedom.
The kinetic energy of a single molecule along the x-axis, the y-axis, and the z-axis is given as
 , along the x-axis
, along the x-axis
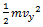 , along the y-axis
, along the y-axis
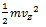 , along the z-axis
, along the z-axis
When the gas is at thermal equilibrium, the average kinetic energy is denoted as
 ,along the x-axis
,along the x-axis
 , along the y-axis
, along the y-axis
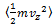 , along the z-axis
, along the z-axis
According to the kinetic theory of gases, the average kinetic energy of a molecule is given by,
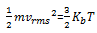
where Vrms is the root-mean-square velocity of the molecules, Kb is the Boltzmann constant and T is the temperature of the gas.
The mono-atomic gas has three degrees of freedom, so the average kinetic energy per degree of freedom is given by 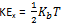
If a molecule is free to move in space, it needs three coordinates to specify its location, thus, it possesses three translational degrees of freedom. Similarly, if it is constrained to move in a plane, it possesses two translational degrees of freedom and if it is a straight line, it possesses one translational degree of freedom. In the case of a triatomic molecule, the degree of freedom is 6. And the kinetic energy of the per molecule of the gas is given as,
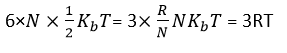

Molecules of a mono-atomic gas like argon and helium have only one translational degree of freedom. The kinetic energy per molecule of the gas is given by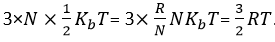 The diatomic gases such as O2 and N2 which have three translational degrees of freedom can rotate only about their center of mass. Since, they have only two independent axes of rotation, as the third rotation is negligible, due to its 2-D structure. Thus, only two rotational degrees of freedom are considered. The molecule thus has two rotational degrees of freedom, each of which contributes a term to the total energy consisting of transnational energy t and rotational energy.
The diatomic gases such as O2 and N2 which have three translational degrees of freedom can rotate only about their center of mass. Since, they have only two independent axes of rotation, as the third rotation is negligible, due to its 2-D structure. Thus, only two rotational degrees of freedom are considered. The molecule thus has two rotational degrees of freedom, each of which contributes a term to the total energy consisting of transnational energy t and rotational energy.
In the video, the first degree of monoatomic, diatomic and triatomic gases are explained.

To learn more about the law of equipartition of energy, the relation between the law of equipartition of energy, and the degree of freedom of a gas molecule, download BYJU’S The Learning App.




Byju classes is most important for jee advance